

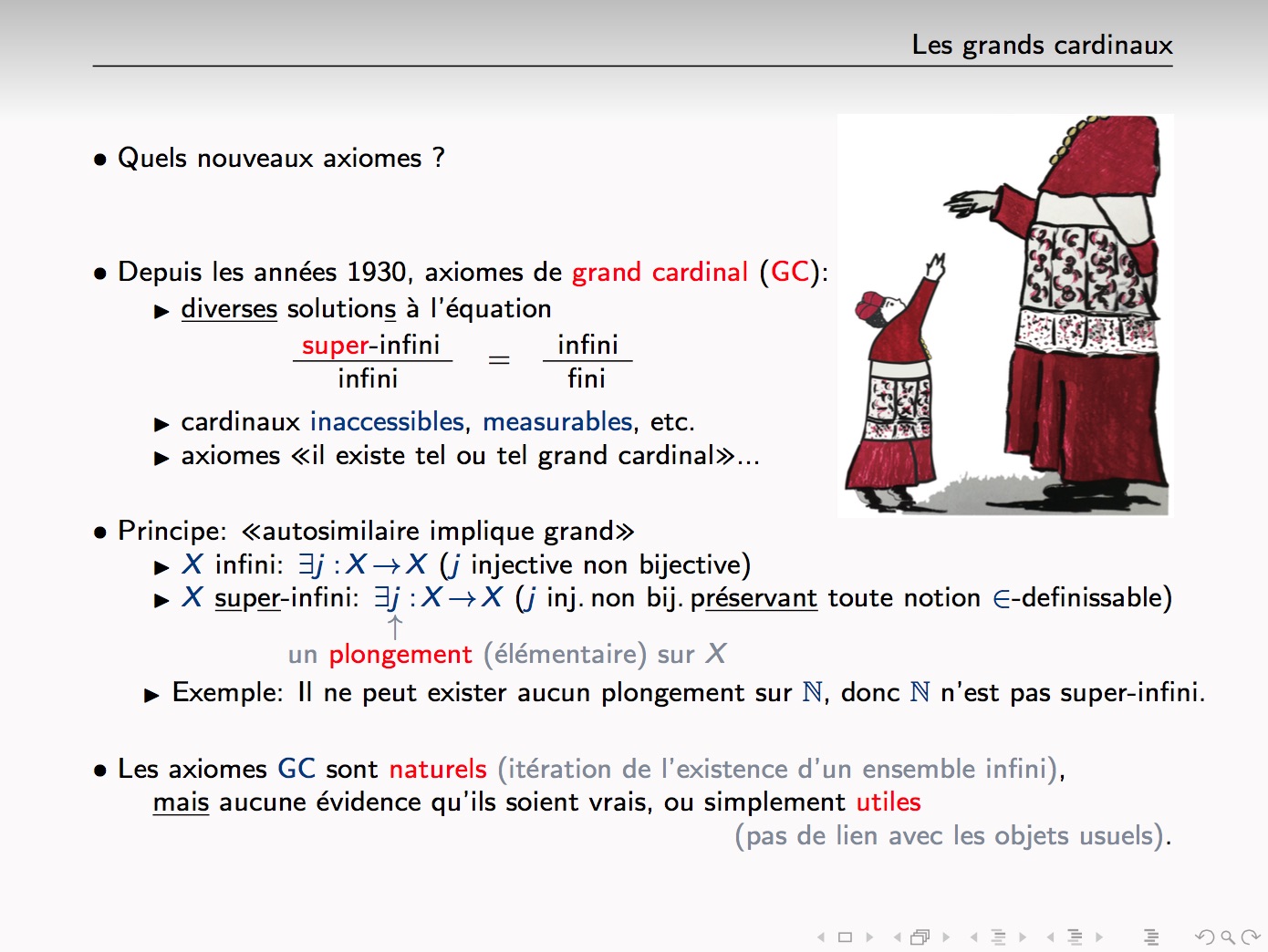
On présentera quelques résultats de la théorie des ensembles récente, avec un accent sur l'hypothèse du continu et la possibilité de résoudre la question après les résultats négatifs bien connus de Godel et Cohen, et sur les tables de Laver, qui sont des structures finies explicites, dont certaines propriétés combinatoires simples n'ont été établies jusqu'à présent que grâce à des axiomes de grand cardinal (non démontrables), une situation très paradoxale.

|
|
| Video en streaming (54') via Youtube | Transparents en .pdf
avec défilement (4.1 Mo), sans défilement (3.3 Mo) |
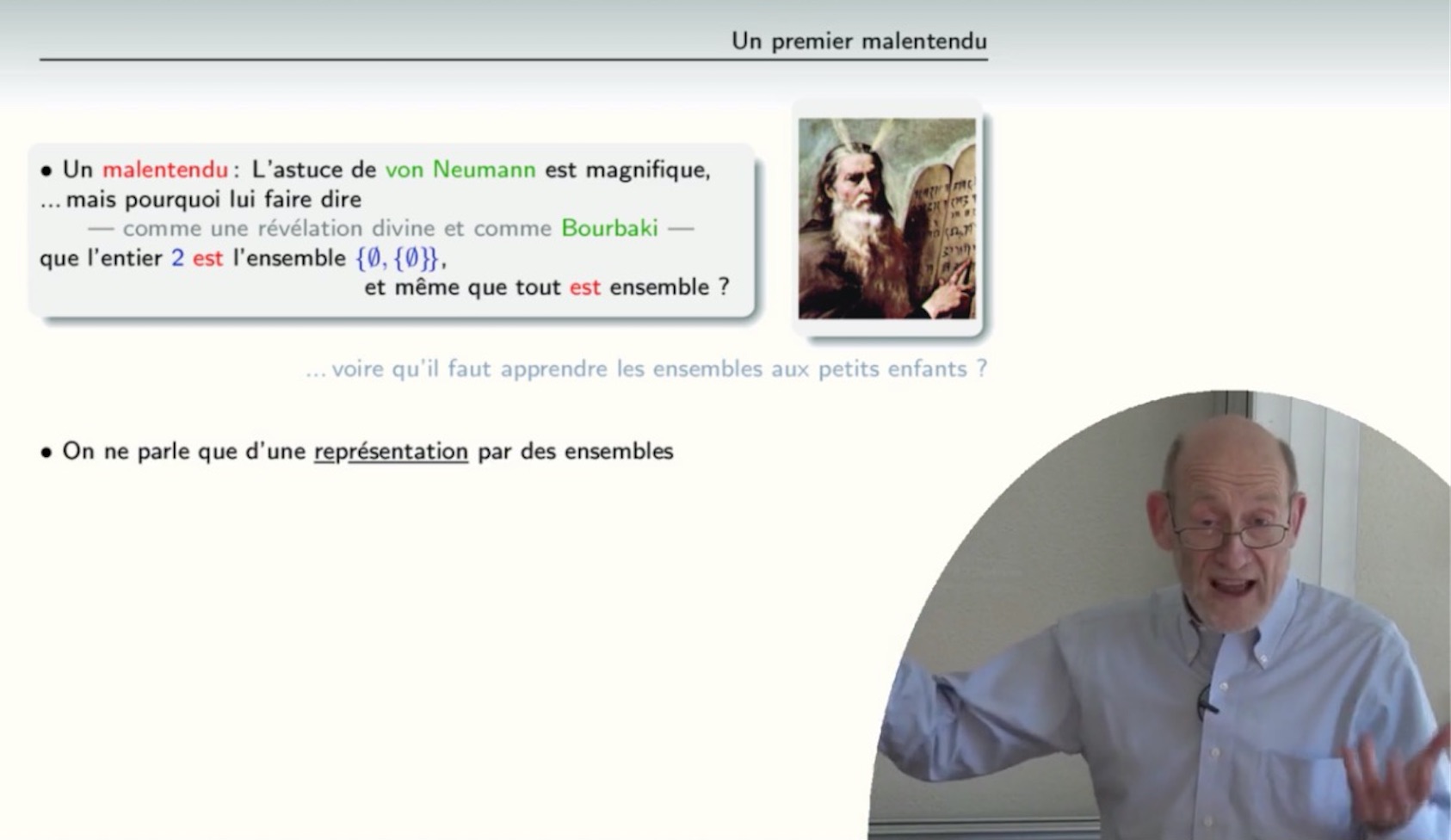
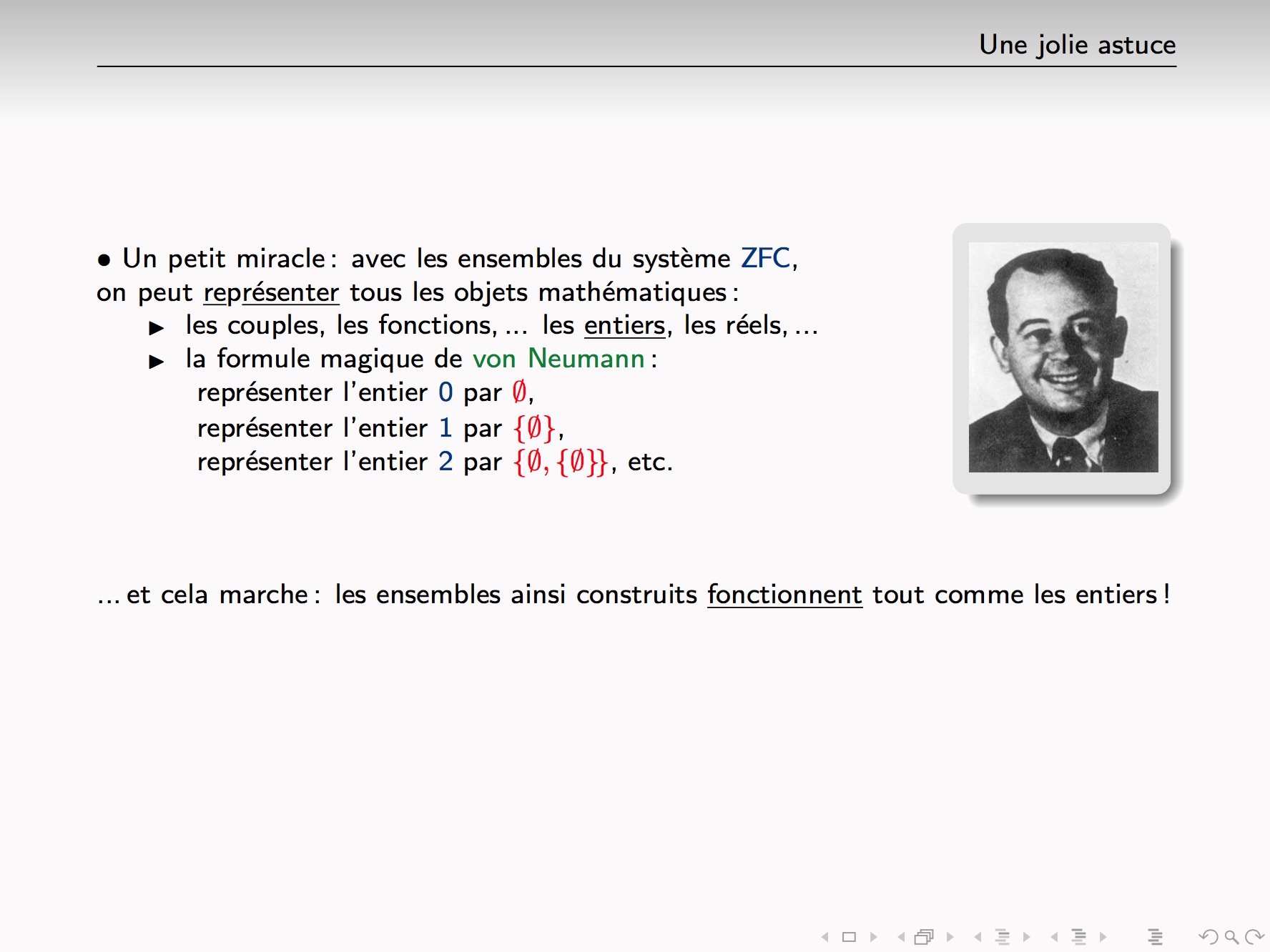
Non, il n'y a aucune raison de croire que l'entier 2 est l'ensemble {Ø, {Ø}}...
Non, il n'y a aucune raison de croire que la non-prouvabilithé de l'hypothèse du continu à partir de ZFC indique que le problème du continu ne sera jamais résolu...
|
|
|
Video en streaming (5') : via Rennes ou via Youtube |
Transparents en .pdf (650 Ko) |
We present a few results of modern Set Theory, with a special emphasis on the Continuum Hypothesis and the possibility of solving the question after the well known negative results of Godel and Cohen, and on Laver tables, which are explicit finite structures, some simple combinatorial properties of which have so far only been proved using (unprovable) large cardinal axioms, a very paradoxical situation.
Earlier version, not mentioning Laver tables but with more details about the Continuum Hypothesis (Strasbourg, Sep. 2011; Brussels, Feb. 2012; StAndrews, May 2012; Paris, Dec. 2013; Clermont, Feb. 2014; Goettingen, Jun. 2014; Vancouver, Jul. 2014; Lille, Dec. 2014, ...)
Il y a longtemps, une bien étrange maladie envahit les écoles et les lycées de France, la théorie des ensembles. Personne n'en mourut, mais grandes furent la perplexité et l'incompréhension, et bien des gens en gardèrent une durable rancœur contre les mathématiques. Heureusement, l'épidémie s'éteignit d'elle-même au bout de quelques années, les professeurs et leurs élèves retrouvèrent le nord, et on finit par oublier ce qui, un temps, avait créé un si grand émoi. C'est sur cette histoire qu'on reviendra ici, pour chercher à comprendre comment la magnifique aventure scientifique lancée à la fin du dix-neuvième siècle par un visionnaire, Georg Cantor, et développée au vingtième par les génies que furent Kurt Gödel et Paul Cohen a pu, par une sorte de malentendu dû à ses succès eux-mêmes, se transformer en un dogme abscons envahissant jusqu'à l'enseignement élémentaire. L'aventure au demeurant n'est pas terminée, et on essaiera également d'expliquer un peu ce qu'est vraiment, aujourd'hui comme au temps de Cantor, la théorie des ensembles, à savoir une élaboration de la notion de l'infini, cette chose mystérieuse et fascinante dont les humains partagent l'intuition mais qu'ils comprennent toujours si mal.

|

|
|
Video en streaming (120') : via Science-Action |
Transparents en .pdf : avec défilement (7.8 Mo), sans défilement (4.2 Mo) |
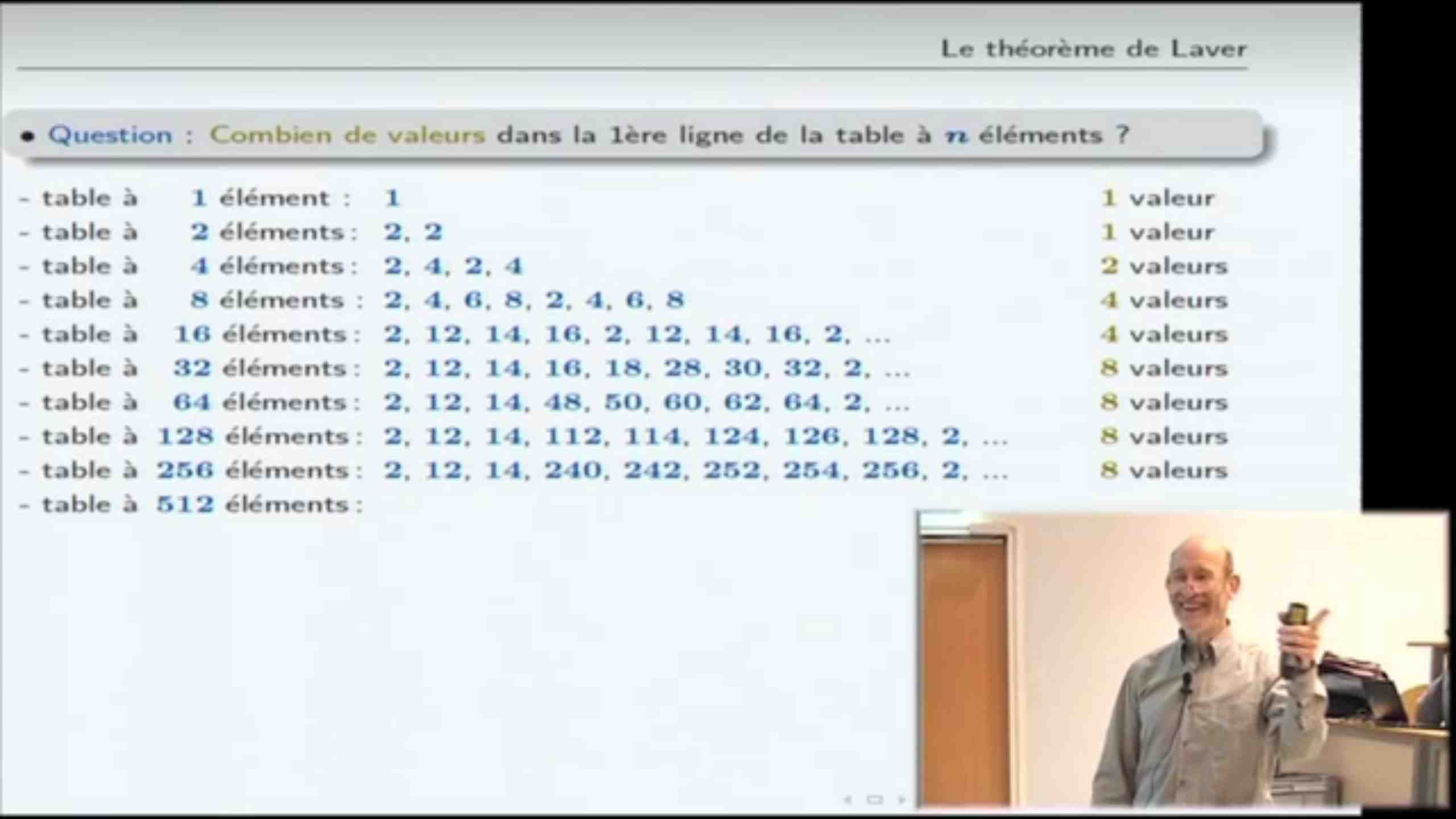
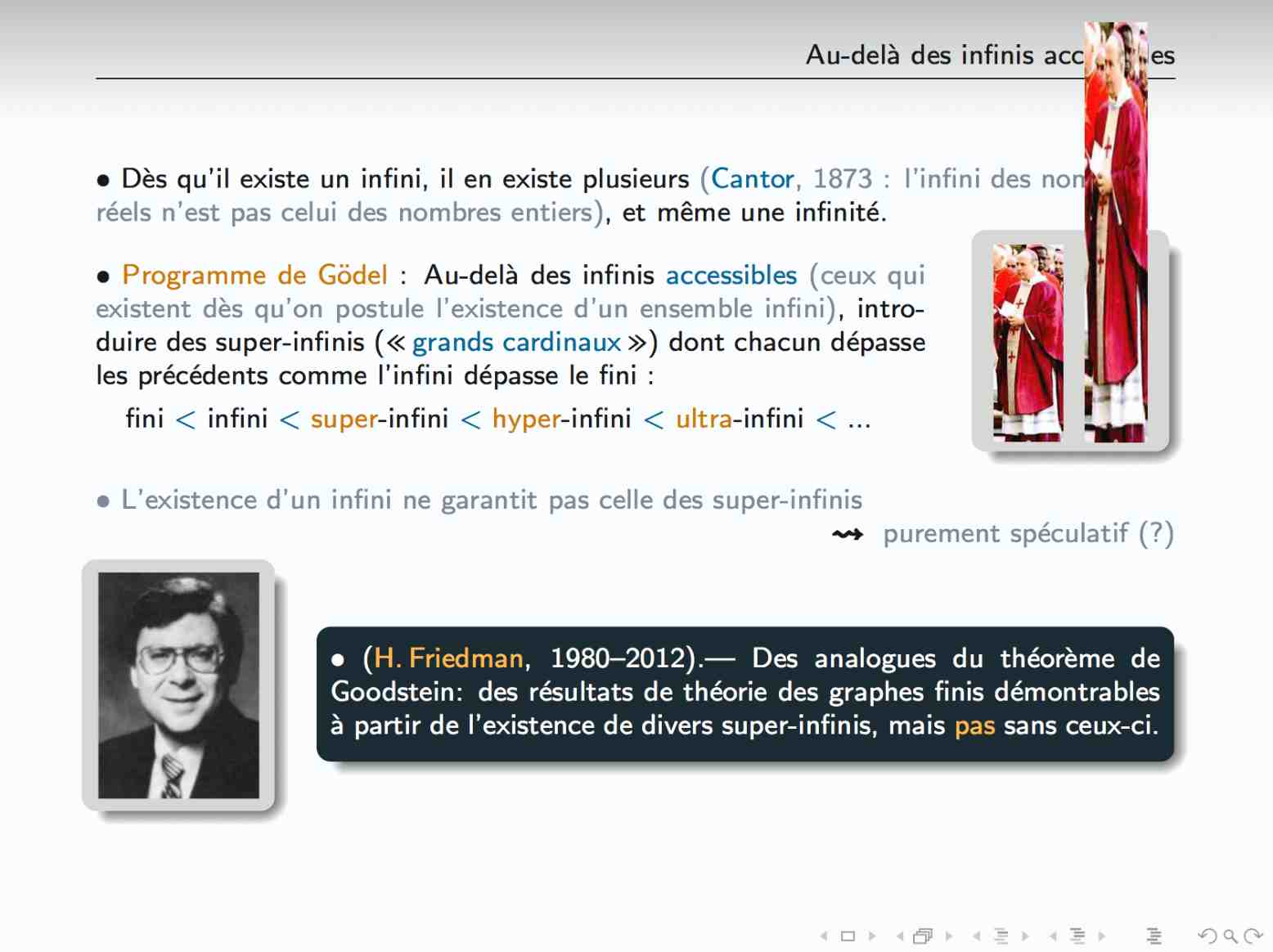
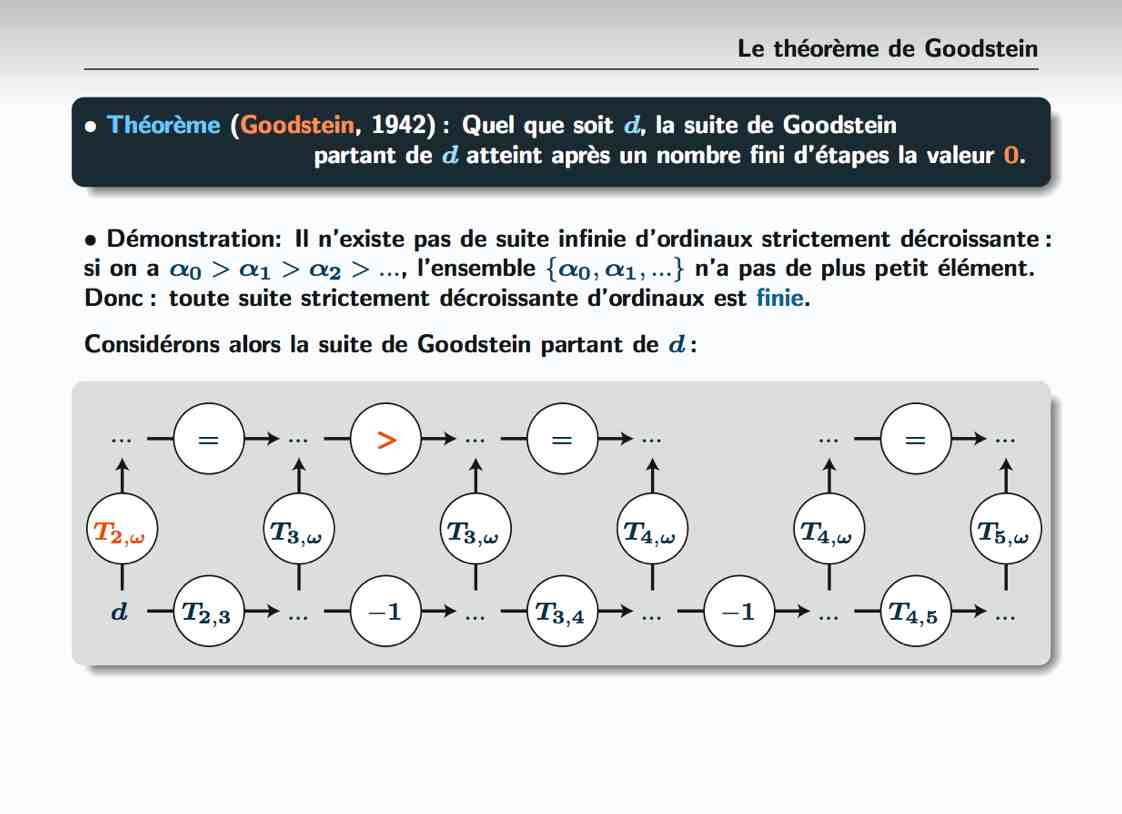
Qu'il faille faire appel à des outils infinis pour démontrer des propriétés des objets infinis n'est pas tres étonnant. Par contre, il est moins intuitif que le passage par l'infini soit déterminant quand il s'agit des propriétés d'objets finis, par exemple des nombres entiers. On montrera pourtant sur quelques exemples que l'utilisation de méthodes ou d'intuitions mettant en jeu l'infini, voire même de très spéculatifs "hyper-infinis", peut permettre de démontrer ou de découvrir des propriétés nouvelles des objets finis.
|
|
|
Video en streaming (62') : via l'université de Rouen |
Transparents en .pdf : avec défilement (4 Mo), sans défilement (2 Mo) |

|
|
| Video en streaming (86') : via la Société Mathématique de France ou Vimeo |
Transparents en .pdf : avec défilement (3.5 Mo), sans défilement (1.1 Mo) |
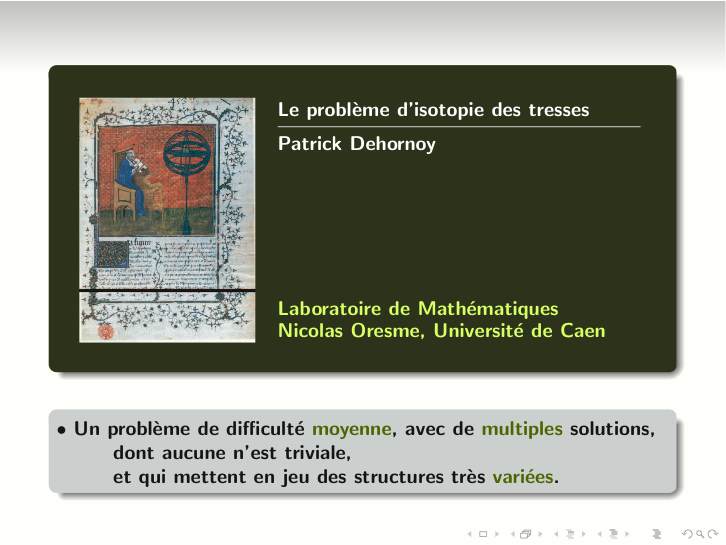
Le problème d'isotopie des tresses est la question de reconnaître si deux diagrammes de tresse peuvent être déformés continûment l'un en l'autre. C'est un problème de difficulté moyenne : ni trop facile — aucune solution n'est triviale — ni trop difficile — des solutions explicites existent. On présentera quelques-unes des (très) nombreuses solutions connues à ce jour, l'intérêt principal étant la multiplicité des approches possibles — algébriques, combinatoires, géométriques, topologiques, etc. — et la diversité des solutions qui en résultent.

|
|
|
Video en .mpg (46' + 66') : Partie 1 (241 Mo), Partie 2 (346 Mo) |
Transparents en .pdf : Partie 1 (2.8 Mo), Partie 2 (5.0 Mo) |
Les tresses n'intéressent pas seulement les coiffeurs et les artistes, elles donnent également lieu a une théorie mathématique profonde qui a des ramifications dans de nombreux domaines: algebre, combinatoire, géométrie, topologie, informatique, et meme physique mathématique et théorie des ensembles. L'exposé vide à montrer qu'il existe un véritable calcul des tresses, qui est une sorte d'extension non commutative du calcul avec les nombres entiers. On presentera quelques développements récents, notamment un algorithme de démelage que chacun peut programmer sur une calculette mais dont l'efficacité étonnante reste pour le moment mystérieuse. On évoquera aussi les possibles applications du calcul des tresses en cryptographie.
In the recent years, several authors began to develop braid-based cryptographical protocols. The talk aims at giving a general overview of this quickly developing field, insisting on the various cryptographical questions one has to address, and on the theoretical and practical problems arising from using braids: choice of a difficult problem (often conjugacy), representation of the data (normal vs. reduced forms), security proofs (lower complexity bounds) and possible attacks.
On montre comment l'étude des grands cardinaux en théorie des ensembles a mené à la construction de systèmes algébriques d'un type nouveau, et, de là, à la découverte d'un ordre total sur les tresses et à celle d'une nouvelle solution particulièrement efficace de leur problème d'isotopie.